MATHEMATICS

What is Number?

An arithmetical value, expressed by a word, symbol, or figure, representing a particular quantity and used in counting and making calculations.

• Numbers are expressed by means of figures- 1,2,3,4,5,6,7,8,9,and 0 called digits.
• 1,2,3,4,5,6,7,8,9 are called significant digits.
• 0 is called insignificant digits.

Types of Number

The main types of numbers used in school mathematics are listed below:

• Natural Numbers (N), (also called positive integers, counting numbers, or natural numbers); They are the numbers {1, 2, 3, 4, 5, …}
• Whole Numbers (W). This is the set of  natural numbers, plus zero, i.e., {0, 1, 2, 3, 4, 5, …}
• Integers (Z). This is the set of all whole numbers plus all the negatives (or opposites) of the natural numbers, i.e., {… ,- 2, -1, 0, 1, 2, …}
• Rational numbers (Q). This is all the fractions where the top and bottom numbers are integers; e.g., 1/2, 3/4, 7/2, ⁻4/3, 4/1 [Note: The denominator cannot be 0, but the numerator can be].
• Real numbers (R), (also called measuring numbers or measurement numbers). This includes all numbers that can be written as a decimal. This includes fractions written in decimal form e.g., 0.5, 0.75 2.35, -0.073, 0.3333, or 2.142857. It also includes all the irrational numbers such as π, √2 etc. Every real number corresponds to a point on the number line.

Discrete and continuous numbersThe above types of numbers can be split up into discrete or continuous numbers.The first four of the above (N, W, Z and Q) are referred to as discrete. This means that they are separate and distinct entities. In fact each of these sets is  countable.The last set, (R), cannot be counted. This is because they are continuous. Between any two real numbers, however close they may be, there are infinitely more real numbersD

What is Number System?

A number system is a system of writing for expressing numbers. It is the mathematical notation for representing numbers of a given set by using digits or other symbols in a consistent manner. It provides a unique representation to every number and represents the arithmetic and algebraic structure of the figures. It also allows us to operate arithmetic operations like addition, subtraction, and division.

Different number systems are mentioned below.

1. Decimal number system (Base- 10)
2. Binary number system (Base- 2)
3. Octal number system (Base-8)
4. Hexadecimal number system (Base- 16)

Decimal Number System

Decimal number system has base 10 because it uses ten digits from 0 to 9. In decimal number system, the positions successive to the left of the decimal point represent units, tens, hundreds, thousands and so on.

Every position shows a particular power of the base (10). For example, the decimal number 1457 consists of the digit 7 in the units position, 5 in the tens place, 4 in the hundreds position, and 1 in the thousands place whose value can be written as

(1×1000) + (4×100) + (5×10) + (7×1)

(1×10³) + (4×10²) + (5×10¹) + (7×1)

1000 + 400 + 50 + 7

1457

Base 2 Number System

Base 2 number systems are also known as Binary number system wherein, only two binary digits exist, i.e., 0 and 1. Specifically, the usual base-2 is a radix of 2. The figures described under this system are known as binary numbers which are the combination of 0 and 1. For example, 110101 is a binary number.

We can convert any system into binary and vice versa.

For Example, to write (14)₁₀ as binary number

Solution:

(14)₁₀ = 1110₂

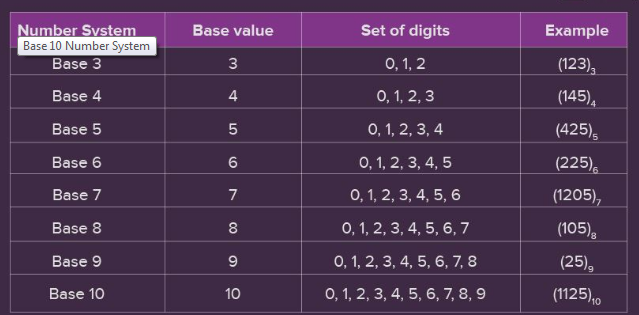
Base 10 Number System

This system is expressed in decimal numbers. The base to the decimal is 10. This shows that there are ten symbols, 0 to 9. Similarly, the system using the symbols 0, 1, two will be of base 3, four symbols will be of base 4 and so on.

Prime number A number other than 1 is called a prime numbers if it is divisible only by 1 and itself.

Composite number Numbers greater then 1 which are not prime are known as composite number e.g-4,6,8,9,10,12

Note:-

• 1 is neither prime nor composite
• 2 is only even number which is prime
• There are 25 prime number between 1 to 100.

Co-primes : Two numbers a and b are said to be co-primes, if their H.C.F. is 1. e.g., (2, 3), (4, 5), (7, 9), (8, 11), etc. are co-primes,

To test whether a given number is prime number or not

Take an integer larger then the approximate square root of the number. Let it be x. Test the divisibility of the given number by every prime number less than x. If it is not divisible by any of them then it is prime number, otherwise it is a composite number.

Even Number : The number which is divisible by 2 is known as an even number e.g. 2,4,8,12,24,28……. It is also of the form 2n(where n=whole number)

Odd Number: The number which is not divisible by 2 is known as an odd number, e.g-3,9,11,17,19……

Consecutive Numbers: A series of numbers in which each is greater then that which precceds it by 1 is called a series of consecutive numbers, e.g.6,7,8or 13,14,15 or 101,102,103,104

.TESTS OF DIVISIBILITY

1. Divisibility By 2 : A number is divisible by 2, if its unit’s digit is any of 0, 2, 4, 6, 8. Ex. 84932 is divisible by 2, while 65935 is not.

2. Divisibility By 3 : A number is divisible by 3, if the sum of its digits is divisible by 3. Ex.592482 is divisible by 3, since sum of its digits = (5 + 9 + 2 + 4 + 8 + 2) = 30, which is divisible by 3. But, 864329 is not divisible by 3, since sum of its digits =(8 + 6 + 4 + 3 + 2 + 9) = 32, which is not divisible by 3.

3. Divisibility By 4 : A number is divisible by 4, if the number formed by the last two digits is divisible by 4. Ex. 892648 is divisible by 4, since the number formed by the last two digits is 48, which is divisible by 4. But, 749282 is not divisible by 4, since the number formed by the last tv/o digits is 82, which is not divisible by 4.

4. Divisibility By 5 : A number is divisible by 5, if its unit’s digit is either 0 or 5. Thus, 20820 and 50345 are divisible by 5, while 30934 and 40946 are not. 5. Divisibility By 6 : A number is divisible by 6, if it is divisible by both 2 and 3. Ex. The number 35256 is clearly divisible by 2. Sum of its digits = (3 + 5 + 2 + 5 + 6) = 21, which is divisible by 3. Thus, 35256 is divisible by 2 as well as 3. Hence, 35256 is divisible by 6.

6. Divisibility By 8 : A number is divisible by 8, if the number formed by the last three digits of the given number is divisible by 8. Ex. 953360 is divisible by 8, since the number formed by last three digits is 360, which is divisible by 8. But, 529418 is not divisible by 8, since the number formed by last three digits is 418, which is not divisible by 8.

7. Divisibility By 9 : A number is divisible by 9, if the sum of its digits is divisible by 9. Ex. 60732 is divisible by 9, since sum of digits * (6 + 0 + 7 + 3 + 2) = 18, which is divisible by 9. But, 68956 is not divisible by 9, since sum of digits = (6 + 8 + 9 + 5 + 6) = 34, which is not divisible by 9.

8. Divisibility By 10 : A number is divisible by 10, if it ends with 0. Ex. 96410, 10480 are divisible by 10, while 96375 is not.

9. Divisibility By 11 : A number is divisible by 11, if the difference of the sum of its digits at odd places and the sum of its digits at even places, is either 0 or a number divisible by 11. Ex. The number 4832718 is divisible by 11, since : (sum of digits at odd places) – (sum of digits at even places) (8 + 7 + 3 + 4) – (1 + 2 + 8) = 11, which is divisible by 11.

10. Divisibility By 12 ; A number is divisible by 12, if it is divisible by both 4 and 3. Ex. Consider the number 34632. (i) The number formed by last two digits is 32, which is divisible by 4, (ii) Sum of digits = (3 + 4 + 6 + 3 + 2) = 18, which is divisible by 3. Thus, 34632 is divisible by 4 as well as 3. Hence, 34632 is divisible by 12.

11. Divisibility By 14 : A number is divisible by 14, if it is divisible by 2 as well as 7.

12. Divisibility By 15 : A number is divisible by 15, if it is divisible by both 3 and 5.

13. Divisibility By 16 : A number is divisible by 16, if the number formed by the last 4 digits is divisible by 16. Ex.7957536 is divisible by 16, since the number formed by the last four digits is 7536, which is divisible by 16.

14. Divisibility By 24 : A given number is divisible by 24, if it is divisible by both 3 and 8. 15. Divisibility By 40 : A given number is divisible by 40, if it is divisible by both 5 and 8. 16. Divisibility By 80 : A given number is divisible by 80, if it is divisible by both 5 and 16.

Note : If a number is divisible by p as well as q, where p and q are co-primes, then the given number is divisible by pq. If p arid q are not co-primes, then the given number need not be divisible by pq, even when it is divisible by both p and q. Ex. 36 is divisible by both 4 and 6, but it is not divisible by (4×6) = 24, since 4 and 6 are not co-primes.